Use The Chart To Multiply The Binomial By The Trinomial
Use The Chart To Multiply The Binomial By The Trinomial - Using the distributive property to find the product (y−4x) (y2+4y+16) results in a polynomial of the form y3+4y2+ay−4xy2−axy−64x. What is the value of a in the. Web to multiply a binomial by a trinomial, multiply each term in the binomial by each term in the trinomial. The expression (y + 3) (y squared. Lasts = (2 • 4 ) = 8. Outers = (3 • 4 ) = 12 x. The expressions that are represented using unknown variables, constants. Web step 1) multiply the first, outer, inner and last pairs. Use 3 and 8 as the last terms of the binomials. The letters foil stand for first, outer, inner, last. Web using the distributive property, each term in the binomial must be multiplied by each of the terms in the trinomial. The expressions that are represented using unknown variables, constants. In this article, we'll review how to multiply these binomials. Web multiply using the distributive property: What is the product?, the polynomial x3 + 8 is equal to and more. Which polynomial is the correct product? X ( 2 x 2 − 5 x + 8) + 3 ( 2 x 2 − 5 x + 8) x\color {red} {. Web multiply using the distributive property: Web use the chart to multiply the binomial by the trinomial. For our first examples, we will show you two ways to organize all. Web = 1 ( x 2) + 1 ( − 5 x) + 1 ( − 6) + x ( x 2) + x ( − 5 x) + x ( − 6) notice the pattern. Web step 1) multiply the first, outer, inner and last pairs. What is the value of a in the. \displaystyle {\left ( {x}+ {11}\right)}. Web (4y − 3)(2y2 + 3y − 5), use the chart to multiply the binomial by the trinomial. Web in mathematics, monomials, binomials, trinomials and polynomials are all algebraic expressions. We can place them in the. Web learn how to multiply a binomial and a trinomial using the distributive property and different strategies. Which polynomial is the correct product? Use the chart to multiply the binomial by the trinomial. Web using the distributive property, each term in the binomial must be multiplied by each of the terms in the trinomial. Outers = (3 • 4 ) = 12 x. Then outer means multiply the outermost terms in the product. for more information go. Web use m and n as. What is the value of a in the. \underbrace { (x+3)}_ { (x+m)}\underbrace { (x+8)}_ { (x+n)} check by multiplying the. = x 2 − 5 x. Web use m and n as the last terms of the factors. See examples, videos, and tables of polynomial products. \underbrace { (x+3)}_ { (x+m)}\underbrace { (x+8)}_ { (x+n)} check by multiplying the. See examples, videos, and tables of polynomial products. For example, x − 2 and x − 6 are both binomials. Web using the distributive property, each term in the binomial must be multiplied by each of the terms in the trinomial. What is the value of a. Outers = (3 • 4 ) = 12 x. The only factors of 3 x 2 3 x 2 are 1 x, 3 x. Web step 1) multiply the first, outer, inner and last pairs. Web = 1 ( x 2) + 1 ( − 5 x) + 1 ( − 6) + x ( x 2) + x (. The only factors of 3 x 2 3 x 2 are 1 x, 3 x. For example, x − 2 and x − 6 are both binomials. Use the chart to multiply the binomial by the trinomial. Web we know the first terms of the binomial factors will multiply to give us 3 x 2. Inners = (2 • 2. For example, x − 2 and x − 6 are both binomials. Web step 1) multiply the first, outer, inner and last pairs. Then outer means multiply the outermost terms in the product. for more information go. Use 3 and 8 as the last terms of the binomials. First means multiply the terms which occur first in each binomial. Web = 1 ( x 2) + 1 ( − 5 x) + 1 ( − 6) + x ( x 2) + x ( − 5 x) + x ( − 6) notice the pattern. In this article, we'll review how to multiply these binomials. You need a way to organize this. For example, x − 2 and x − 6 are both binomials. Web (4y − 3)(2y2 + 3y − 5), use the chart to multiply the binomial by the trinomial. X ( 2 x 2 − 5 x + 8) + 3 ( 2 x 2 − 5 x + 8) x\color {red} {. Web step 1) multiply the first, outer, inner and last pairs. The expression (y + 3) (y squared. The letters foil stand for first, outer, inner, last. Using the distributive property to find the product (y−4x) (y2+4y+16) results in a polynomial of the form y3+4y2+ay−4xy2−axy−64x. Use 3 and 8 as the last terms of the binomials. Inners = (2 • 2 ) = 4 x. We multiplied each term in the binomial by each term in the trinomial. Web multiply using the distributive property: Outers = (3 • 4 ) = 12 x. Step 2) simplify by adding the terms.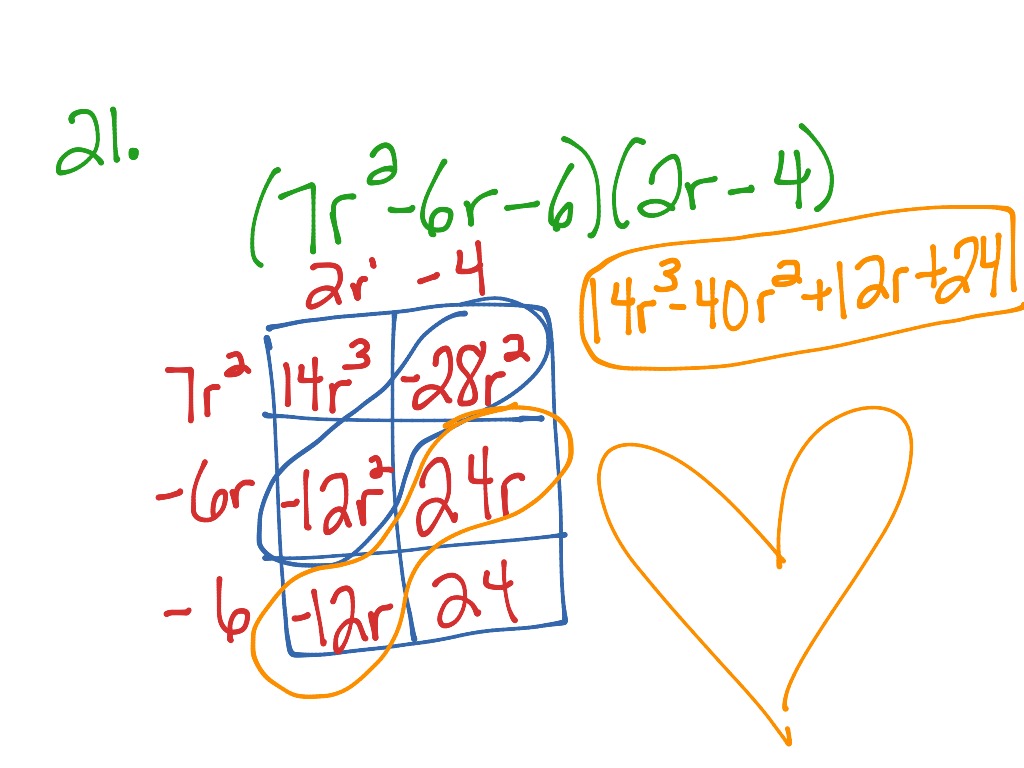
ShowMe multiplying a binomial and trinomial

Guide to multiplying a binomial and a trinomial 2

Example Multiply a Binomial Times a Trinomial YouTube
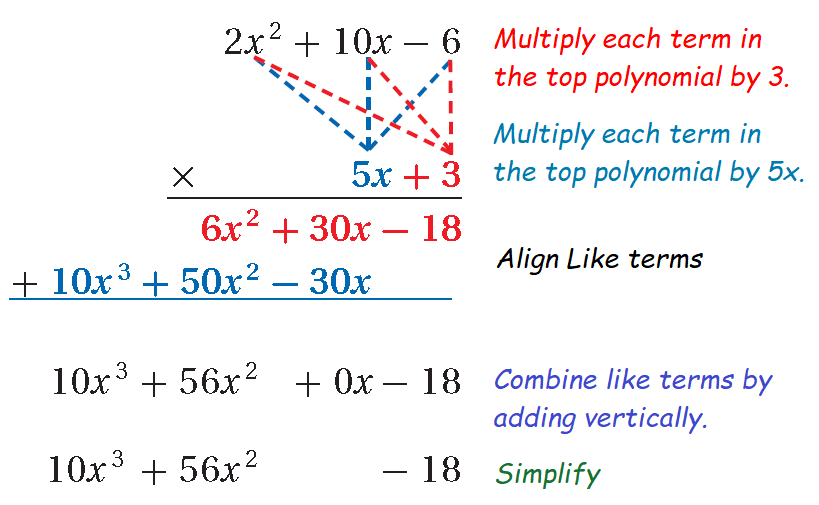
Multiplying a Binomial by a Trinomial
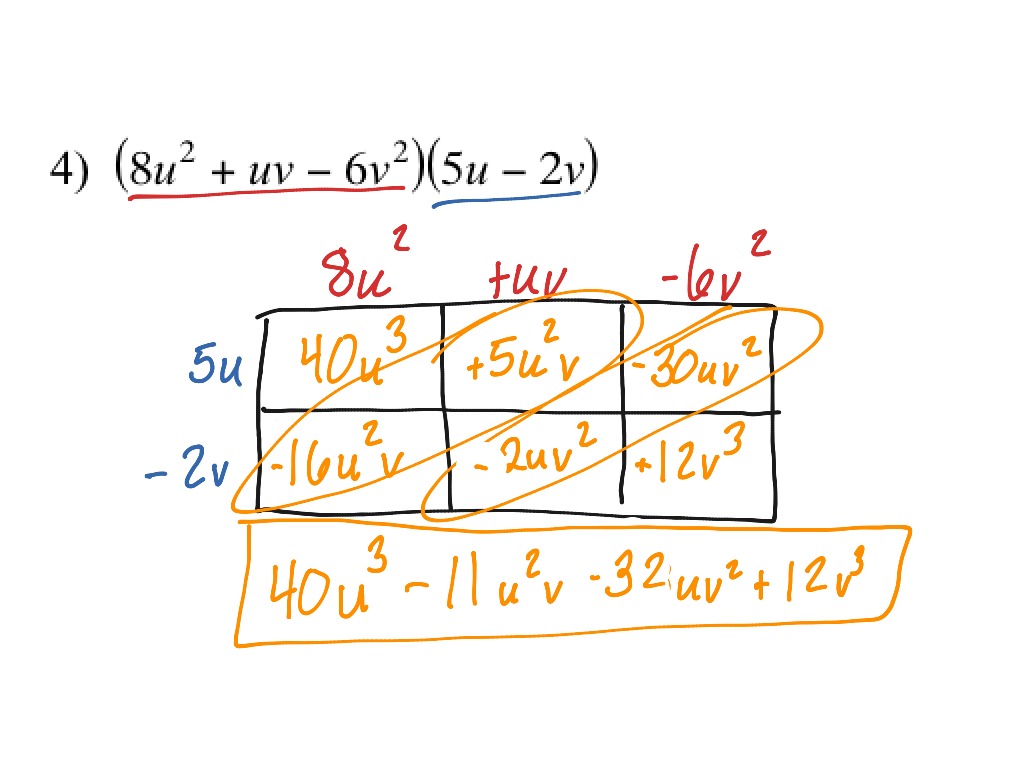
Multiplying Trinomials by Binomials Math ShowMe

(New Version Available) Polynomial Multiplication Involving Binomials

Use The Chart To Multiply The Binomial By The Trinomial.

Question Video Multiplying a Binomial by a Trinomial Nagwa

Question Video Multiplying a Binomial by a Trinomial Nagwa

Use the chart to multiply the binomial by the trinomial. Which
First Means Multiply The Terms Which Occur First In Each Binomial.
Then Outer Means Multiply The Outermost Terms In The Product. For More Information Go.
Web To Multiply A Binomial By A Trinomial, Multiply Each Term In The Binomial By Each Term In The Trinomial.
For Our First Examples, We Will Show You Two Ways To Organize All.
Related Post: