First Derivative Sign Chart
First Derivative Sign Chart - The first derivative test can be used to locate. On what intervals is 𝑓 increasing or decreasing? Graph of derivative to original function. Web explain how the sign of the first derivative affects the shape of a function’s graph. In this question, we are given the curve of 𝑦 = 𝑓 ′ ( 𝑥) and asked to find the intervals on which 𝑓 ( 𝑥) is increasing. How do you find values of t in which the speed of the particle is increasing if he position of a particle moving along a line is given by s(t) = 2t3 − 24t2 + 90t + 7 for t ≥ 0? Resourcefunction [ derivativesigncharts] [ f, x] creates a grid of sign charts for f(x), f' (x) and f'' (x). Web the top graph is the original function, f (x), and the bottom graph is the derivative, f’ (x). State the first derivative test for critical points. They help you find maxima, minima and saddle points. You’re looking to say something about the function f ( x) based on its derivative f ′ ( x). Web what information does the first derivative tell you? This is the sign chart for our function: In a sign chart, we pick a test value at each interval that is bounded by the points we found in step 2 and. Web you can use sign charts to analyze the behavior of a function. Web the graph of the derivative 𝑓 ′ of a function 𝑓 is shown. Web we create a first derivative sign chart to summarize the sign of \(f'\) on the relevant intervals, along with the corresponding behavior of \(f\text{.}\) figure \(\pageindex{4}\). Web f' is the derivative of. The stationary points are written on the sign diagram. Web 4.5.1 explain how the sign of the first derivative affects the shape of a function’s graph. Web we create a first derivative sign chart to summarize the sign of f' on the relevant intervals along with the corresponding behavior of f. Web you can use sign charts to analyze the. They help you find maxima, minima and saddle points. Web f' is the derivative of f, and f'' is the second derivative of f, which is the first derivative of f'. Explain the concavity test for a function over an open interval. Resourcefunction [ derivativesigncharts] [ f, x] creates a grid of sign charts for f(x), f' (x) and f''. Explain the concavity test for a function over an open interval. Resourcefunction [ derivativesigncharts] [ f, x] creates a grid of sign charts for f(x), f' (x) and f'' (x). This calculus video tutorial provides a basic introduction into the first derivative test. Graph of derivative to original function. Here, it’s important to keep your head in the game. What information can we determine about the function using the first derivative? They help you find maxima, minima and saddle points. The stationary points are written on the sign diagram. You’re looking to say something about the function f ( x) based on its derivative f ′ ( x). What do you notice about each pair? Now determine a sign chart for the first derivative, f ' : What information can we determine about the function using the first derivative? Web you can use sign charts to analyze the behavior of a function. Web we create a first derivative sign chart to summarize the sign of \(f'\) on the relevant intervals, along with the corresponding behavior. To establish a sign chart (number lines) for f ' , first set f ' equal to zero and then solve for x. Web explain how the sign of the first derivative affects the shape of a function’s graph. This calculus video tutorial provides a basic introduction into the first derivative test. Web we create a first derivative sign chart. The first derivative test can be used to locate. On what intervals is 𝑓 increasing or decreasing? How do you find the interval in which the function f (x) = 2x3 + 3x2 + 180x is increasing or decreasing? Web the first derivative of the function f(x), which we write as f0(x) or as df dx, is the slope of. Web what follows is the first derivative sign chart for a function which has a positive derivative to the left of x = 0 , a negative derivative to the right of x = 0, and zero derivative at x = 0. Web f' is the derivative of f, and f'' is the second derivative of f, which is the. Graph of derivative to original function. Now determine a sign chart for the second derivative, f '' : What do you notice about each pair? Web 4.5.1 explain how the sign of the first derivative affects the shape of a function’s graph. They help you find maxima, minima and saddle points. Web this can be done in many ways, but we like using a sign chart. The stationary points are written on the sign diagram. Web the graph of the derivative 𝑓 ′ of a function 𝑓 is shown. In the regions between these points, a positive sign is written when the function is increasing and a negative sign is written when the function is decreasing. This is the sign chart for our function: 4.5.3 use concavity and inflection points to explain how the sign of the second derivative affects the shape of. On what intervals is 𝑓 increasing or decreasing? Web the first derivative of the function f(x), which we write as f0(x) or as df dx, is the slope of the tangent line to the function at the point x. What information can we determine about the function using the first derivative? Web 493k views 6 years ago new calculus video playlist. You’re looking to say something about the function f ( x) based on its derivative f ′ ( x).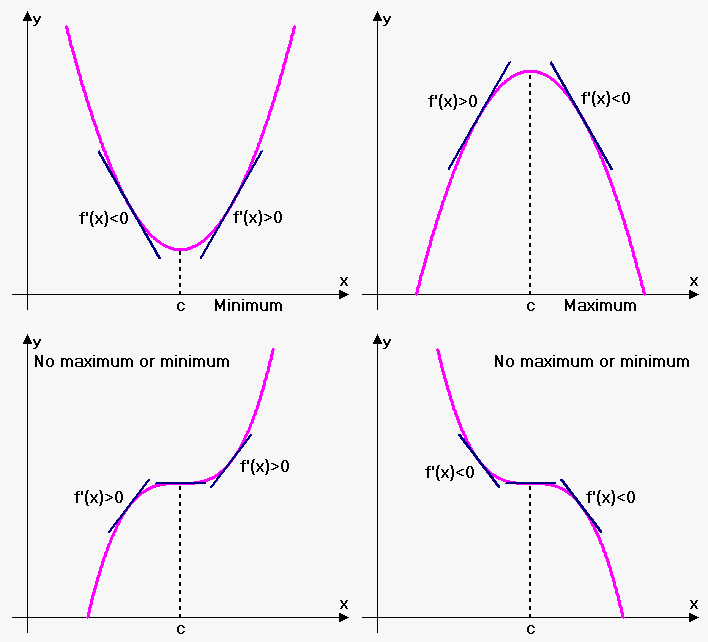
First Derivative Test eMathHelp

Derivative Rules Cheat Sheet Calculus Ace Tutors Blog
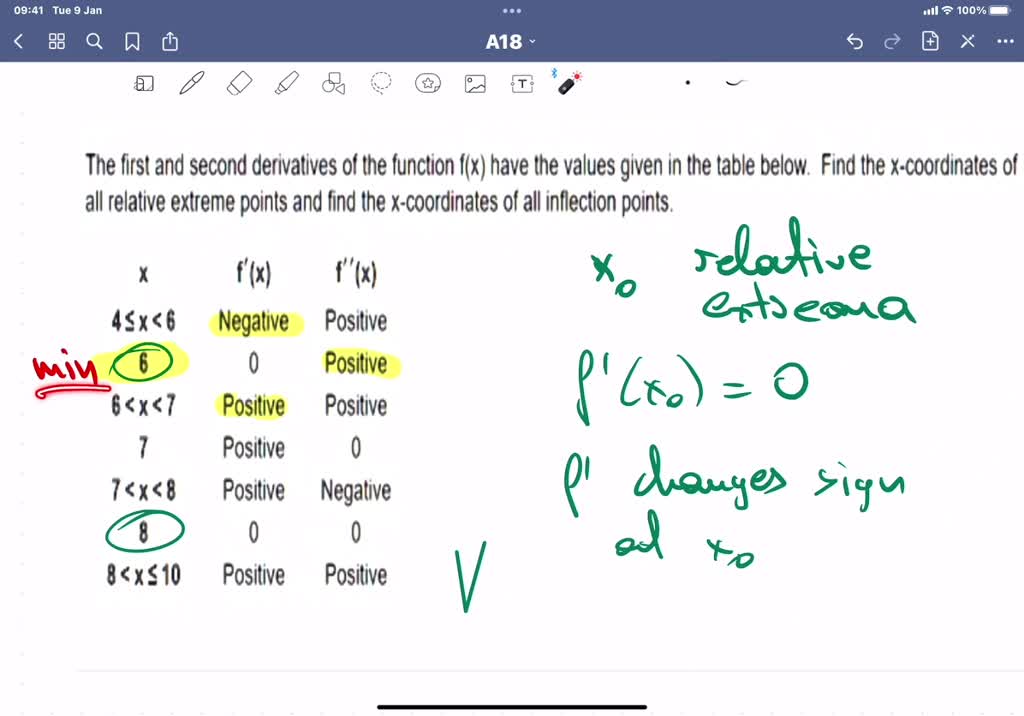
SOLVED Below you see the first derivative sign chart (the sign chart
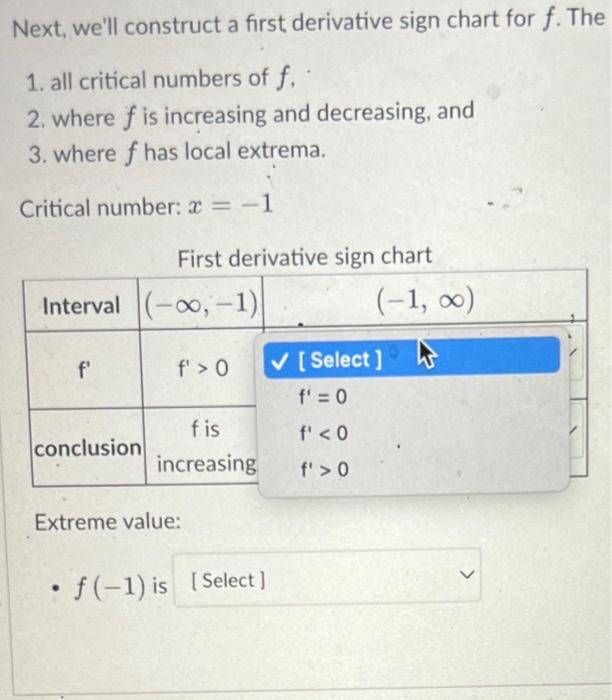
next well construct a first derivative sign chart for f the 1 all

How to Understand Sign Diagrams
![[Math] How to identify the graph of a function and the graphs of its](https://i.stack.imgur.com/vze2T.png)
[Math] How to identify the graph of a function and the graphs of its

Making and Interpreting Sign Charts (First and Second Derivatives

Chart Of Derivatives

3.3 First Derivative Test / Slope Shuford's Site
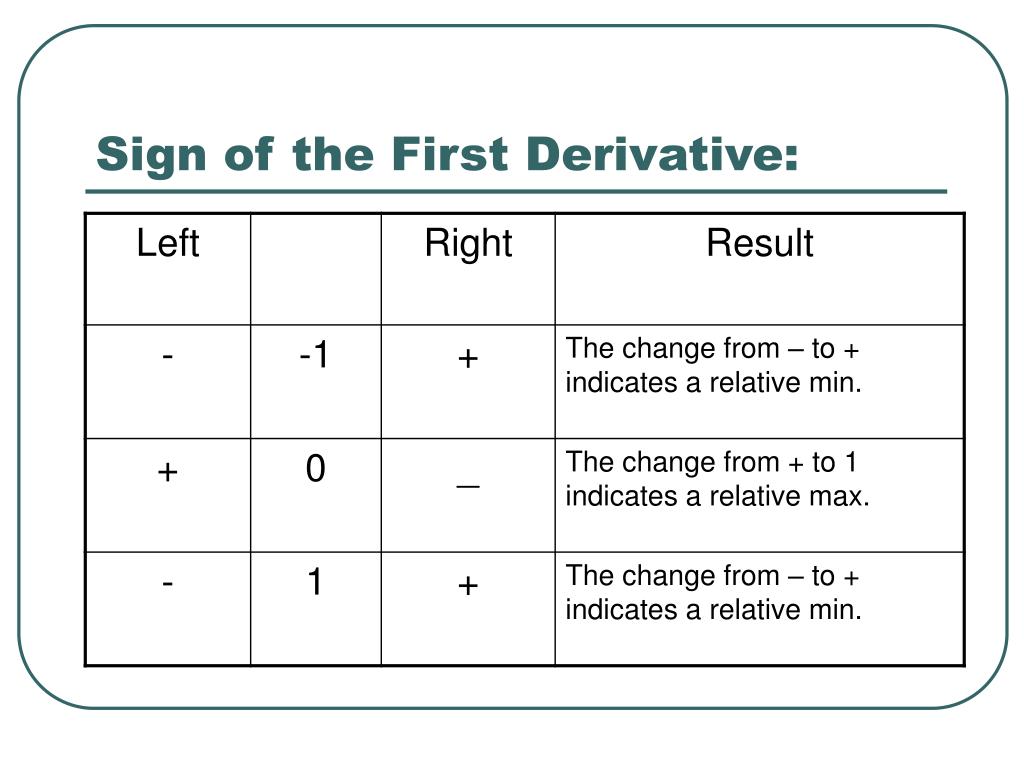
PPT Applications of Derivatives PowerPoint Presentation, free
How Do You Find Values Of T In Which The Speed Of The Particle Is Increasing If He Position Of A Particle Moving Along A Line Is Given By S(T) = 2T3 − 24T2 + 90T + 7 For T ≥ 0?
State The First Derivative Test For Critical Points.
Use Concavity And Inflection Points To Explain How The Sign Of The Second Derivative Affects The Shape Of A Function’s Graph.
In This Question, We Are Given The Curve Of 𝑦 = 𝑓 ′ ( 𝑥) And Asked To Find The Intervals On Which 𝑓 ( 𝑥) Is Increasing.
Related Post: