Draw Two Different Rectangles With An Area Of 16

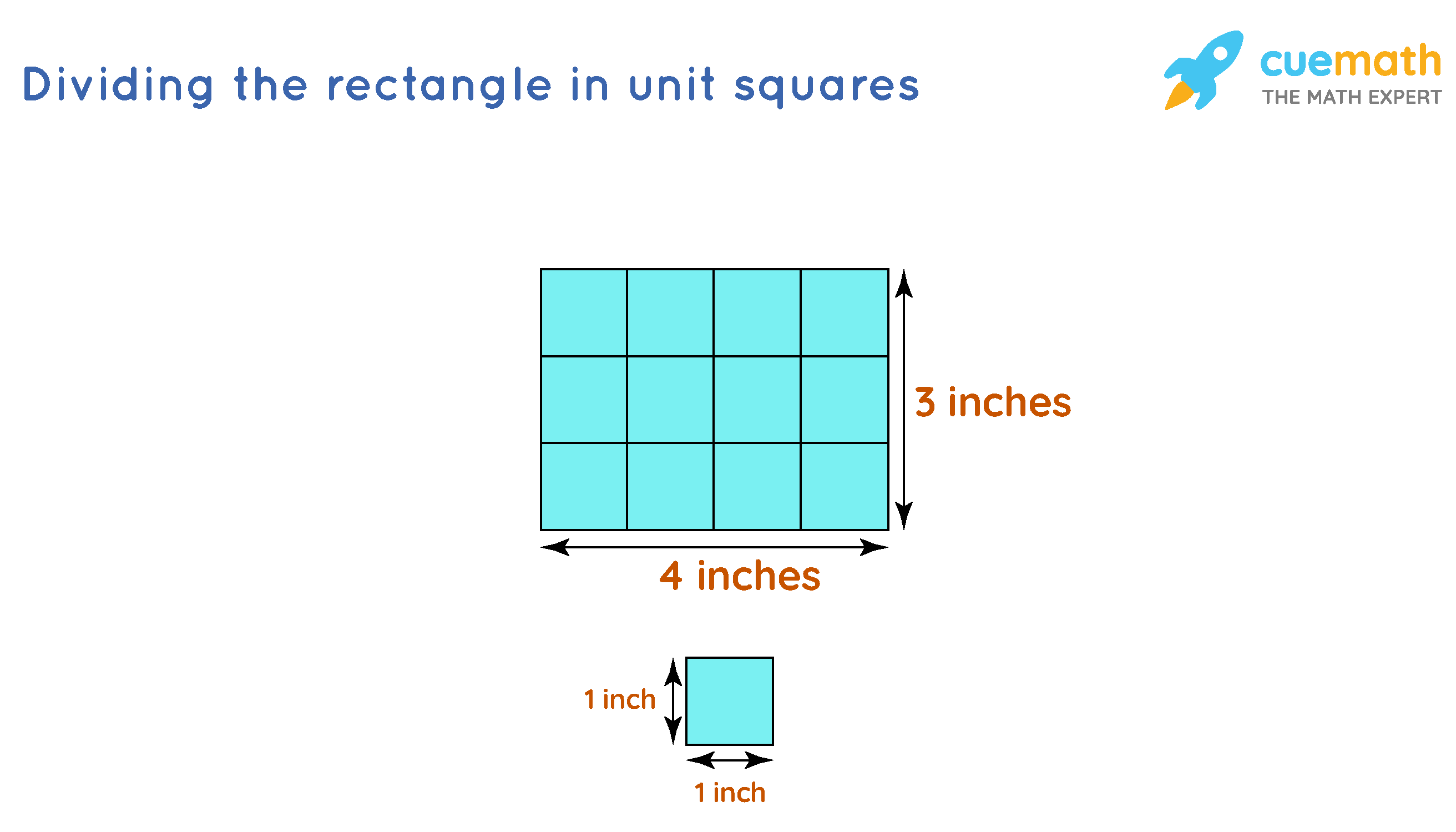
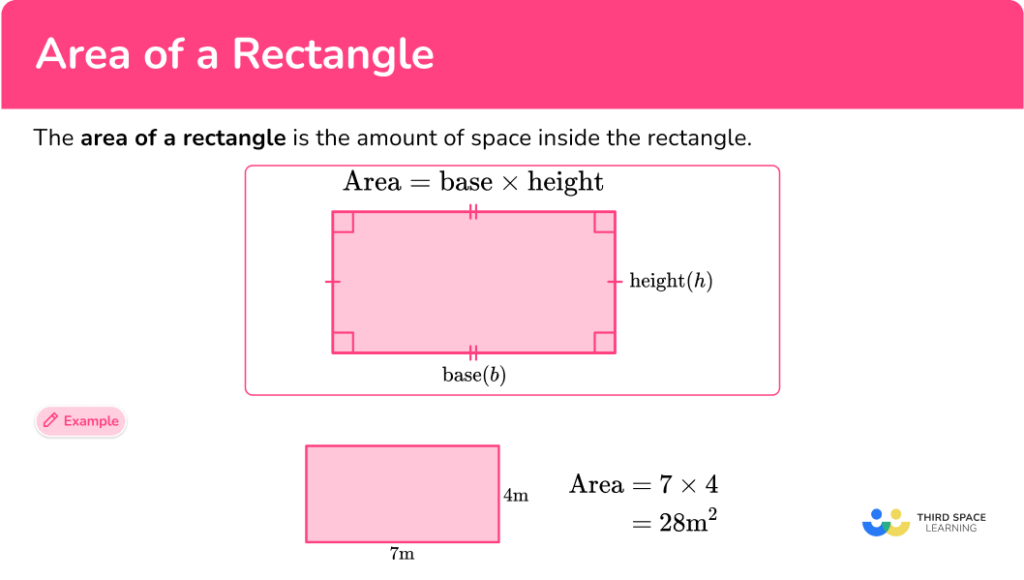
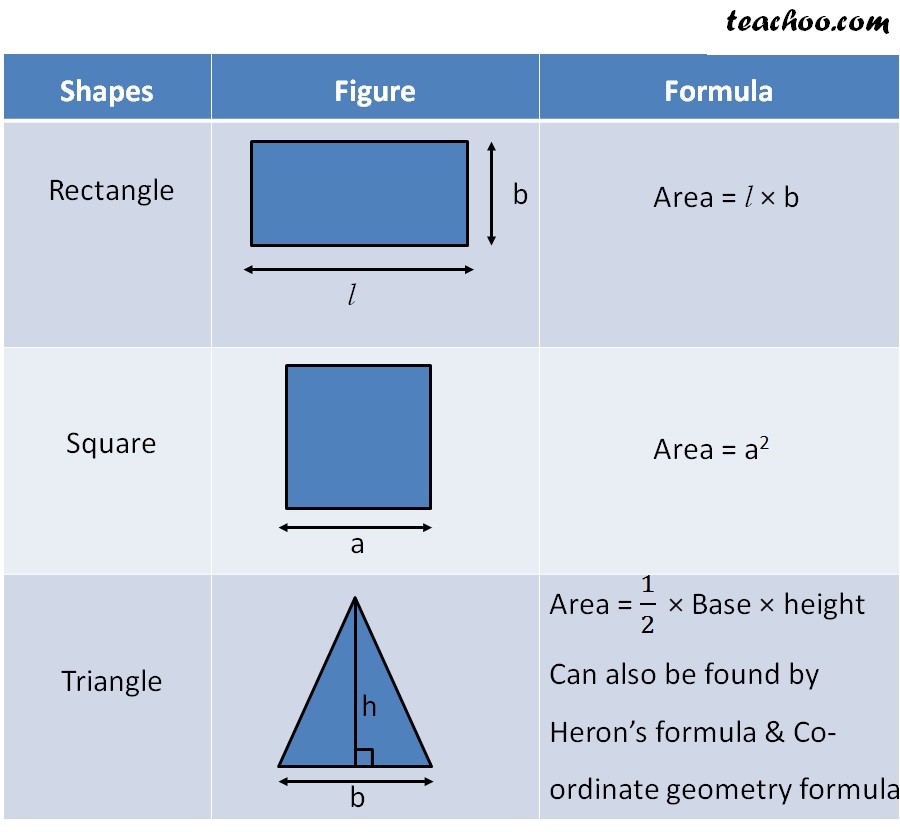
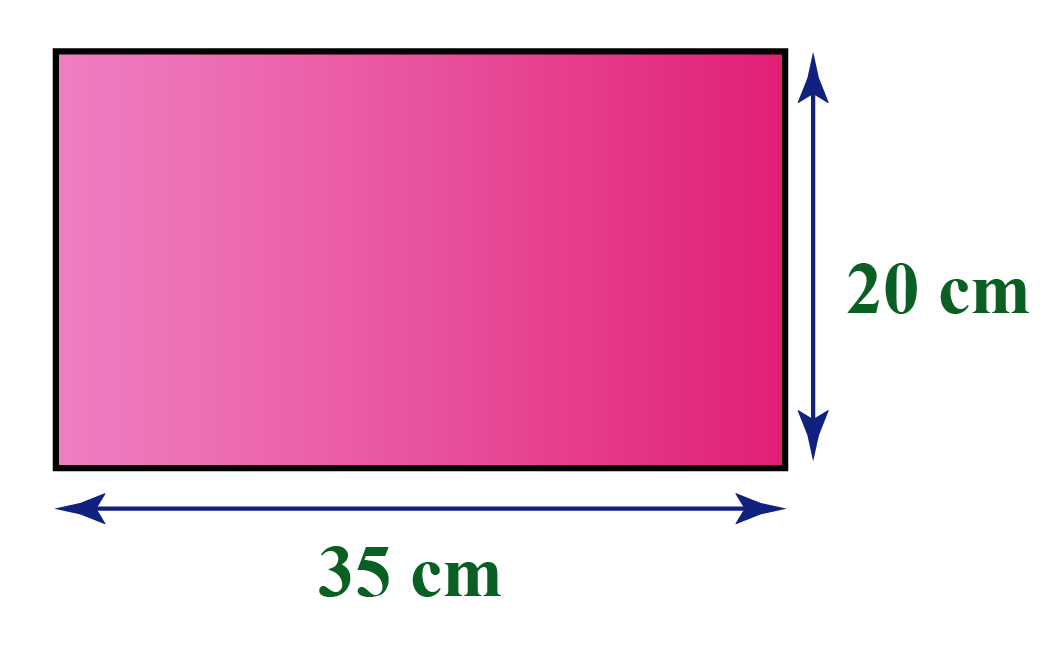
Draw Two Different Rectangles With An Area Of 16 - Explain why it is possible to draw more than two different rectangles with an area of 36 square units, but it is not possible to draw more than two different rectangles with an area of 15 square units. P = 2 × (l + w) lesson 20 homework. The perimeter is 4(5) = 20in and the area is 52 = 25 in2. Web create rectangles with a given area (practice) | khan academy. These can all be dimensions of the different rectangles. A = 0.5 × a × b × sin(γ) or. Web draw two different rectangles (see below) on the board and ask the students if there is any way that these two rectangles could have the same perimeter (discussion time). A = s 2 = 75 i n 2 s = 75 = 5 3 i n. “can both these rectangles have a perimeter of 16 units?” think, pair, share. Then write an addition or multiplication equation for each area.

Area of Rectangle Definition, Formulas, Examples, Facts Cuemath

How are they the same? Web so we’ve learned that the area of two shapes can be equal, but they can have different perimeters. Area = 2 x 8 = 16 square units. A = s 2 = 75 i n 2 s = 75 = 5 3 i n. Using unit squares, we'll measure their areas, emphasizing the importance.

Rectangle area formula hisdop

Draw and label two different rectangles, each with perimeters of 20 units. Identify the area in square units. For a rectangle, the bigger the perimeter, the bigger the area. Using unit squares, we'll measure their areas, emphasizing the importance of a unit square for measuring various shapes. As a stretch activity, challenge children to use irregular shapes instead of just.

draw two different rectangles with an area of 16 plywoodvanshelvingplans

Areas of rectangles with the same perimeter. Do the rectangles have the same area? Use the etool below to draw different rectangles. Cut out the unit squares above. Web each of these is one square unit, so our rectangle covers one, two, three, four, five, six, seven, eight square units.

Area of a rectangle formula dopgplus

Label the side lengths of each rectangle. Draw and shade three different rectangles with an area of 24 square units. A = s 2 = 75 i n 2 s = 75 = 5 3 i n. • i can find the factor pairs for a number. Think of all the different factors of 36.

Draw two different rectangles with a perimeter of Gauthmath

4.6 (6 ratings) create an account to view solutions. Estimate to draw your rectangles below. We know that eight times two is 16 and four times four is 16. Draw and shade three different rectangles with an area of 24 square units. Anya draws a few rectangles, but then she stops drawing and starts looking for pairs of numbers that.

Area of a Rectangle Math Steps, Examples & Questions

Cut out the unit squares above. Perimeter = (1 + 16 + 1 + 16) = 34 units. P = 2 × (l + w) lesson 20 homework. Pose a problem a tile company tiled a wall using square tiles. Find the area of each rectangle.

Area of Different Shapes (with Formula) Mensuration Class 8

Find the area of each rectangle. Web so we’ve learned that the area of two shapes can be equal, but they can have different perimeters. Draw two different rectangles with the area listed. Explain we could start with a side of 1 unit. Do the rectangles have the same area?

Drawing rectangles with certain perimeters and areas YouTube

These can all be dimensions of the different rectangles. “can both these rectangles have a perimeter of 16 units?” think, pair, share. Use the etool below to draw different rectangles. P = 2 × (l + w) lesson 20 homework. No sides should be 6 units long.

Area of Rectangle Definition, Formulas, Examples, Facts Cuemath

A = a × b. Find the area of each rectangle. We know that eight times two is 16 and four times four is 16. These can all be dimensions of the different rectangles. Web draw two different rectangles (see below) on the board and ask the students if there is any way that these two rectangles could have the.

(PDF) Draw and label the dimensions of two different rectangles

Then write an addition or multiplication equation for each area. Think of all the different factors of 36. P = 2 × (l + w) lesson 20 homework. Use your factors identified to draw on graph paper the 3 rectangles with the factors as the length of each side. Estimate to draw your rectangles below.

From This, P = 4 ( 5 3) = 20 3 I N.

Wayna drew a rectangle with an area of 24 square units. Area = 4 x 4 = 16 square units. A = s 2 = 75 i n 2 s = 75 = 5 3 i n. Web in this worksheet, children should use the squared grid under each question to draw two shapes which have different perimeters but the same given area.

To Find The Perimeter, We Need To Find The Length Of The Sides.

Area = 2 x 8 = 16 square units. Draw area models that show a product. Web so we’ve learned that the area of two shapes can be equal, but they can have different perimeters. Draw two different rectangles with an area of 36 c m 2.

Web Find Two Different Dimensions That The Rectangle Could Be.

Perimeter = (4 + 4 + 4 + 4) = 16 units. Perimeter = (1 + 16 + 1 + 16) = 34 units. Draw two different rectangles with an area of 36 cm2. Web the rectangles have different areas.

Explain Why It Is Possible To Draw More Than Two Different Rectangles With An Area Of 36 Square Units, But It Is Not Possible To Draw More Than Two Different Rectangles With An Area Of 15 Square Units.

We know that eight times two is 16 and four times four is 16. Using unit squares, we'll measure their areas, emphasizing the importance of a unit square for measuring various shapes. Web create rectangles with a given area (practice) | khan academy. Compare your rectangles to your partner’s rectangles.