A Scale Drawing Of A Rectangular Park
A Scale Drawing Of A Rectangular Park - Give an example of how this scale could tell us about measurements in the. Web in the scale drawing, the lengths of the rectangular park are given as 8.4 cm and 3.7 cm. Web given data , let the scale of the rectangular park be 1 cm = 60m. So, for every 1 cm on the drawing, the actual distance is 60 m. The scale drawing has a length of 4.8 cm and a width of. Remember area is a = lw. Other math questions and answers. Web the length of the park in the drawing is 6.6 cm, and the width is 7.9 cm. The amount of time is equal to 1 centimeter. What do you think that means? To find the actual length and width of the park, we need to multiply the drawing measurements. Web understand how a scale drawing is converted into real numbers using the scale factor. The original length is equal to. Perimeter = 2 (l + w) perimeter = 2 (10.1 cm + 8.8 cm) perimeter =. Plot a rectangle on a piece. A(0,0) b(0,2) c(3,2) d(3,0) now choose your scale. The actual park is 30 yards long. The scale drawing has a length of 4.8 cm and a width of. A map of a park says its scale is 1 to 100. (11.1+8.3)* 2=19.4* 2=38.8cm an prestangle parks 1cm=100m so 38.8cm=3880m actual perimeter is 3880 m. On a scale drawing, the dimensions of the park are 12 inches wide by 20 inches long. Remember area is a = lw. A scale drawing of a rectangular park measures 6.5 inches long and 4 inches wide. Web the scale of the drawing is 1 cm = 60 m. What is the scale that was used? So, for every 1 cm on the drawing, the actual distance is 60 m. Web a scale drawing is a drawing of an object that is larger or smaller than, but proportional to, the original object. A town is designing a rectangular park that will be 600 feet by 1000 feet. Now , the perimeter p of rectangle = 2. Web in the scale drawing, the lengths of the rectangular park are given as 8.4 cm and 3.7 cm. Remember area is a = lw. However, based on the scale of 1 cm = 110 m in reality, we have to. A town is designing a rectangular park that will be 600 feet wide by 1000 feet long. What is. Solving a scale drawing word problem. What is the actual area of the park in meters squared? First, we find the perimeter of the scale drawing. Web understand how a scale drawing is converted into real numbers using the scale factor. Perimeter = 2 (l + w) perimeter = 2 (10.1 cm + 8.8 cm) perimeter =. Remember area is a = lw. However, based on the scale of 1 cm = 110 m in reality, we have to. The actual park is 30 yards long. Web for example, here is a scale drawing of a park where the scale is 1 cm to 90 m. Web you can use graph paper to help you make scale. A town is designing a rectangular park that will be 600 feet by 1000 feet. The original length is equal to. A map of a park says its scale is 1 to 100. Web the length of the park in the drawing is 6.6 cm, and the width is 7.9 cm. On a scale drawing, the dimensions of the park. Give an example of how this scale could tell us about measurements in the. A scale drawing of a rectangular park is 5 inches wide and 7 inches long. A(0,0) b(0,2) c(3,2) d(3,0) now choose your scale. Web given data , let the scale of the rectangular park be 1 cm = 60m. The scale drawing has a length of. A rectangular shape is what we have here. Figure \(\pageindex{5}\) the rectangle is 10 cm by 4 cm, so the actual. The amount of time is equal to 1 centimeter. Web understand how a scale drawing is converted into real numbers using the scale factor. A scale drawing of a rectangular park is 5 inches wide and 7 inches long. Web you can use graph paper to help you make scale drawings. Web understand how a scale drawing is converted into real numbers using the scale factor. Plot a rectangle on a piece of graph paper at these coordinates: Now , the perimeter p of rectangle = 2 ( length + width ) the length of the rectangular park l =. A town is designing a rectangular park that will be 600 feet by 1000 feet. What do you think that means? Solving a scale drawing word problem. Perimeter = 2 (l + w) perimeter = 2 (10.1 cm + 8.8 cm) perimeter =. Web in the scale drawing, the lengths of the rectangular park are given as 8.4 cm and 3.7 cm. The actual park is 30 yards long. However, based on the scale of 1 cm = 110 m in reality, we have to. Web a scale drawing of a rectangular park is 10 inches wide and 6 inches long. Other math questions and answers. So, for every 1 cm on the drawing, the actual distance is 60 m. What is the actual area of the park in meters squared? On a scale drawing, the dimensions of the park are 12 inches wide by 20 inches long.![[ANSWERED] A scale drawing of a rectangular park is 8 inches long and 5](https://media.kunduz.com/media/sug-question-candidate/20231011185838709243-4709416.jpg?h=512)
[ANSWERED] A scale drawing of a rectangular park is 8 inches long and 5
Solved A scale drawing of a rectangular park had a scale of[algebra
A scale drawing of a rectangular park had a scale CameraMath

A scale drawing of a rectangular park had a scale of 1 cm = 100 m. What

SOLVED A scale drawing of a rectangular park is 5 inches wide and 7

A scale drawing of a rectangular park had a scale of 1 cm = 110 m. 8.6
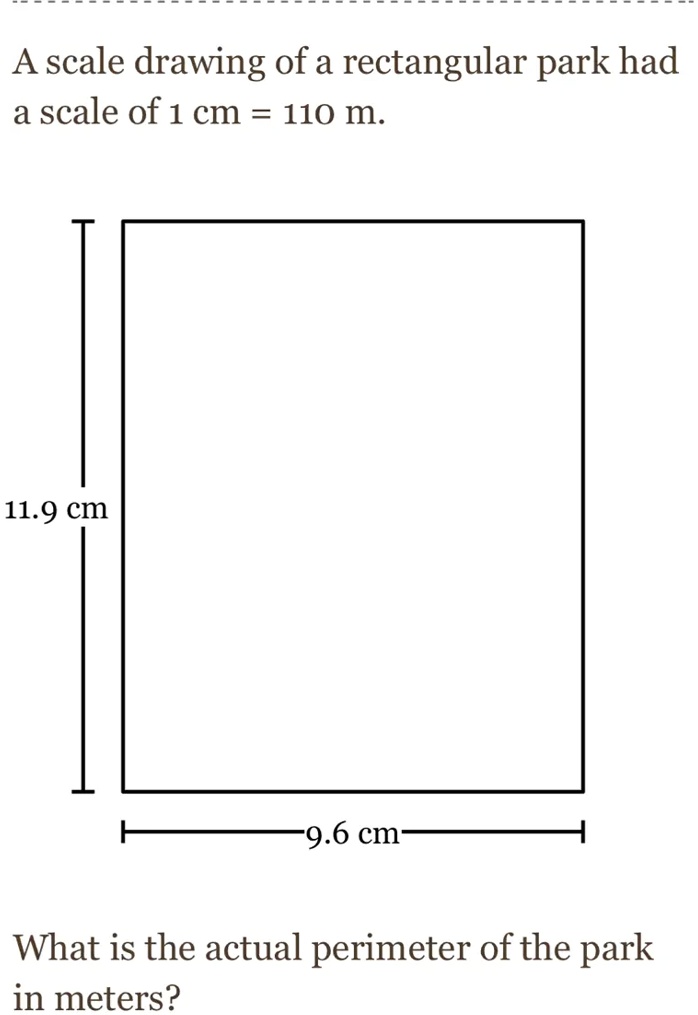
SOLVED A scale drawing of a rectangular park had a scale of 1 cm = 110

How to Draw a Park Really Easy Drawing Tutorial

A rectangular park is to be designed whose breadth is 3m less than its
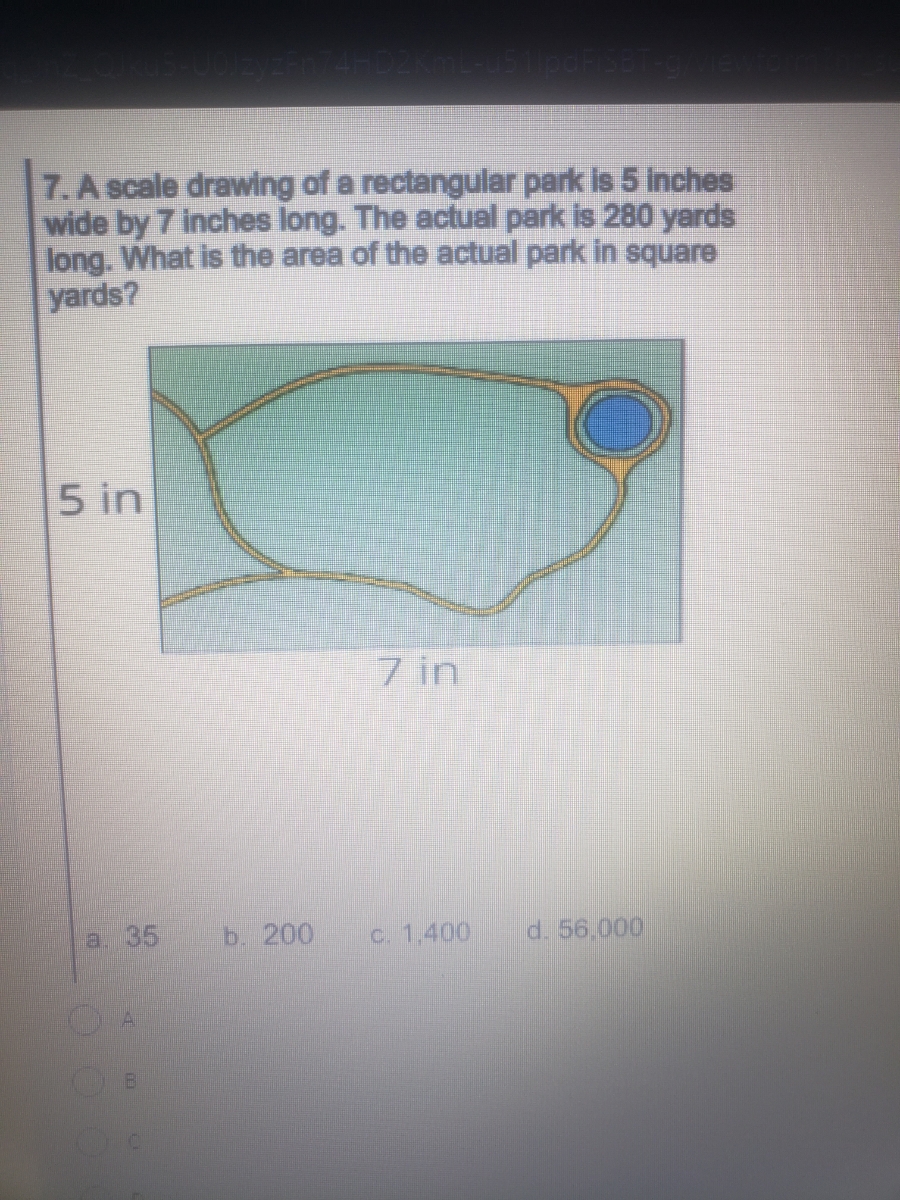
Answered 7. A scale drawing of a rectangular… bartleby
See How We Solve A Word Problem By Using A Scale Drawing And Finding The.
Figure \(\Pageindex{5}\) The Rectangle Is 10 Cm By 4 Cm, So The Actual.
Remember Area Is A = Lw.
Web The Scale Of The Drawing Is 1 Cm = 60 M.
Related Post:
